 LOS NÚMEROS RACIONALES.
LOS NÚMEROS RACIONALES.
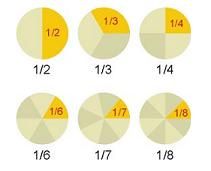 En las matemáticas se conoce el concepto de números racionales para hacer referencia a aquellos indicadores que permiten conocer el cociente entre dos números enteros. La noción de racional proviene de ración (parte de un todo). Los números racionales están formados por los números enteros (que pueden expresarse como cociente: 5= 5/1, 38=38/1) y los números fraccionarios (los números racionales no enteros: 2/5, 8/12, 69/253).
En las matemáticas se conoce el concepto de números racionales para hacer referencia a aquellos indicadores que permiten conocer el cociente entre dos números enteros. La noción de racional proviene de ración (parte de un todo). Los números racionales están formados por los números enteros (que pueden expresarse como cociente: 5= 5/1, 38=38/1) y los números fraccionarios (los números racionales no enteros: 2/5, 8/12, 69/253).
Cada uno de los números enteros posee otro carácter que le sigue; de tal modo que al -1 le sigue el 0 y a éste el 1, sucesivamente, y a su vez entre cada uno de éstos existen infinitos números no racionales.
Los números racionales permiten expresar medidas. Cuando se compara una cantidad con su unidad, se obtiene, por lo general, un resultado fraccionario. Por ejemplo: Si divido una pizza en dos partes, tengo dos mitades. Cada porción será 1/2 de la pizza (una parte de dos). En caso de tomar ambas porciones, volveré a tener la pizza entera (2/2= 1).
Los números racionales pueden ser sumados, restados, multiplicados o divididos (excepto por cero). El resultado de estas operaciones será siempre otro número racional. Como los números enteros pueden ser positivos o negativos, se aplica la Ley de Signos. La forma de concretar las operaciones variará de acuerdo a la existencia o ausencia de igual denominador en las fracciones.
La historia de los números racionales.
Hubo una época en que los números no formaban parte de la vida cotidiana; existió un día en el que fueron descubiertos y durante siglos se creyó que se trataban de un elemento independiente del ser humano y de carácter universal y abstracto (cada número representa la misma cantidad en todos los idiomas y culturas). Sin embargo, no siempre fue así y eso nos permite saber que existió un descubrimiento-creación de los números tal cual hoy lo conocemos y, siendo un producto de la actividad humana, no es perfecto.
En la cultura griega el 0 (cero) no era considerado un número puesto que no podía compararse con algo real, representaba la nada y la nada no existe por tanto lo tenían absolutamente anulado; a su vez, el 1 tampoco tenía carácter numeral pues era con el que se formaban el resto de los números y por ende no podía tomarse en cuenta de forma independiente.
A los comienzos de la humanidad ciertas nociones hoy claramente diferenciables no se entendían como tal. De hecho las medidas de magnitud y numerales se realizaban teniendo en cuenta las diferencias y el contrasta y no las semejanzas y, como es de esperarse, no se trataban de porciones exactas. Podían diferenciar claramente entre un lobo y muchos o entre un pececito diminuto y una ballena, pero no entre objetos de similares magnitud o entre cantidades semejantes.
 Posiblemente hayan sido los pobladores del Antiguo Egipto quienes comenzaron a establecer parámetros claros que definieron a los números racionales tal cual nosotros los conocemos. Los matemáticos de aquella época usaban fracciones unitarias, que son aquellas cuyos denominadores son números enteros positivos. En los casos en que necesitaban fracciones con numeradores no unitarios, los egipcios apelaban a la suma de fracciones unitarias distintas (conocidas como fracción egipcia).
Posiblemente hayan sido los pobladores del Antiguo Egipto quienes comenzaron a establecer parámetros claros que definieron a los números racionales tal cual nosotros los conocemos. Los matemáticos de aquella época usaban fracciones unitarias, que son aquellas cuyos denominadores son números enteros positivos. En los casos en que necesitaban fracciones con numeradores no unitarios, los egipcios apelaban a la suma de fracciones unitarias distintas (conocidas como fracción egipcia).
A partir de aquel momento este aspecto de los conocimientos se consolidó al punto de que hoy nos resulta difícil separar las matemáticas de nuestra vida y, por ende, los números racionales. Sin embargo los apasionados de la filosofía y el origen de las cosas continúan intentando responder a la eterna discusión, ¿son los números racionales algo inventado por el ser humano o pertenecen a una revelación que la propia naturaleza le hizo a nuestra especie en su debido momento?
Son
ejemplos de números racionales:
También
son números racionales los números enteros:
Un
mismo número racional se puede expresar con varias fracciones. Por ejemplo:
De todas estas formas, la primera se llama fracción irreducible y las demás fracciones equivalentes.
Los números racionales son infinitos. Aunque parezca increíble podemos asociar un número natural a cada número racional. Muchas veces los números racionales se expresan como números decimales. Por ejemplo:
 En resumen un número racional es todo valor que puede ser expresado mediante una fracción a/b. Todas las fracciones equivalentes entre sí (8/12 = 4/6 = 2/3) expresan el mismo número racional. Es decir, todo número que se pueda poner en forma de fracción se dice que es un número racional.
En resumen un número racional es todo valor que puede ser expresado mediante una fracción a/b. Todas las fracciones equivalentes entre sí (8/12 = 4/6 = 2/3) expresan el mismo número racional. Es decir, todo número que se pueda poner en forma de fracción se dice que es un número racional.  El -3 es un número entero y racional porque se puede poner en forma de fracción así: -3/1 ¿Para qué sirven?: Los números racionales son parte de la base que todos debemos saber para resolver operaciones matemáticas más complejas que son posteriores a esta y que siempre podremos encontrar en la vida cotidiana. Por ejemplo: al partir un pastel en partes iguales, en la administración del dinero, en ciencias como la física, química y biología, entre otras situaciones de nuestra vida cotidiana, estamos ocupando los números racionales, sin darnos cuenta, ni darle la importancia que se merece.
El -3 es un número entero y racional porque se puede poner en forma de fracción así: -3/1 ¿Para qué sirven?: Los números racionales son parte de la base que todos debemos saber para resolver operaciones matemáticas más complejas que son posteriores a esta y que siempre podremos encontrar en la vida cotidiana. Por ejemplo: al partir un pastel en partes iguales, en la administración del dinero, en ciencias como la física, química y biología, entre otras situaciones de nuestra vida cotidiana, estamos ocupando los números racionales, sin darnos cuenta, ni darle la importancia que se merece.  Podemos clasificar los números racionales de la siguiente forma: NÚMEROS RACIONALES 5/7 es un número racional porque ya está expresado en forma de fracción. 12/4 es un número racional puesto que está expresado en forma de fracción, y además como la división es exacta y da 3, también es un número natural o entero positivo. 0,12121212.... es un número racional porque se puede poner en forma de fracción así: 12/99 Multiplicación y División Denominador común Denominadores distintos Para sumar fracciones con el mismo denominador mantenemos el denominador común y sumamos o restamos los numeradores. En primer lugar se reducen los denominadores a común denominador, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas.
Podemos clasificar los números racionales de la siguiente forma: NÚMEROS RACIONALES 5/7 es un número racional porque ya está expresado en forma de fracción. 12/4 es un número racional puesto que está expresado en forma de fracción, y además como la división es exacta y da 3, también es un número natural o entero positivo. 0,12121212.... es un número racional porque se puede poner en forma de fracción así: 12/99 Multiplicación y División Denominador común Denominadores distintos Para sumar fracciones con el mismo denominador mantenemos el denominador común y sumamos o restamos los numeradores. En primer lugar se reducen los denominadores a común denominador, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas..jpg)





















